Algorithm Note 01: Elementary Sort

• Selection sort
• Insertion sort
• Shell sort

Recently I plan to study the algorithm systematically. I have studied, used and developed several algorithms, but I think I still lack very systematical knowledge of algorithm analysis and design. According to Zhihu’s recommendation, I will fast go through the book: Robert Sedgewick, Algorithm, 4th edition and try to get a sense of the general principle of algorithm analysis and design.

I will write some notes here to record my study which may include the principle, illustration and implementation of of certain algorithms.

Sorting is one of the most important and fundamental problems in algorithm design and analysis.

Selection sort

Principle:

1. Find the smallest item in the array and exchange it with the first entry, then this item is sorted.
2. Find the smallest item in the rest array without the sorted items and exchange it with the 1st item of the rest array.
3. Repeat step 2 until all the items are sorted.

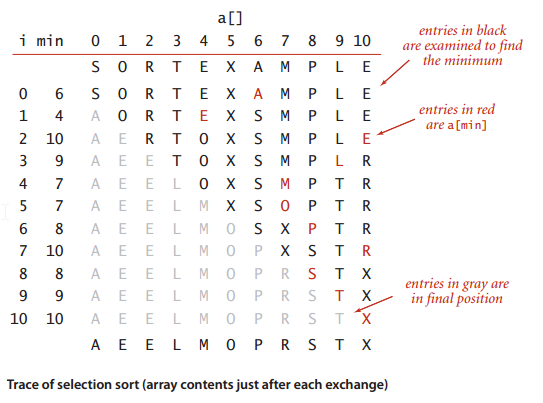
Analysis:

• Suppose we have N items to sort. The first item needs $(N-1)$ comprison, and the ith item needs $(N-i)$ COMPARE. So the algorithm will needs $(N-1)+(N-2)+...+0 = ~N^2/2$ times COMPARE. And each item needs 1 SWAP. In total, the number of comparison and exchange is $N^2/2 + N$.

• The number of computation is fixed in selection sorting. Selection sort needs the least number of exchange $N$.

C++ implementation:

// selection sort
void selectionsort(std::vector<int> &vec)
{
    int n = vec.size();
    for (int i =0; i<n; ++i)
    {
        for (int j =i; j<n; ++j) 
        {
            if (vec[i]>vec[j])
                exchange(vec,j,i);                
        }
    }
}

Insertion sort

Principle:

1. The items to the left of current index are in sorted order but not at the final position.
2. COMPARE current item with the item on its left, SWAP if current item is smaller and continue the COMPARE and SWAP until current item is larger than its left item. So the number of COMPARE dependes on the original order of array, the number of SWAP is one step less.
3. Repeat step 2 until all the items are sorted.

Analysis:

• Insertion sort uses ~$N^2/4$ compares and ~$N^2/4$ exchanges to sort a randomly ordered array of length N with distinct keys, on the average. The worst case is ~$N^2/2$ compares and ~$N^2/2$ exchanges and the best case is $N-1$ compares and 0 exchanges.

• The number of exchanges used by insertion sort is equal to the number of inversions in the array, and the number of compares is at least equal to the number of inversions and at most equal to the number of inversions plus the array size minus 1.

• Insertion sort is an excellent method for partially sorted arrays and is also a fine method for tiny arrays.

C++ implementation:

// insertion sort
void insertionsort(std::vector<int> &vec)
{
    int n = vec.size();
    for (int i = 1; i<n; ++i)
    {
        for (int j=i; j>0 && (vec[j]<vec[j-1]); j--)
        {
            exchange(vec, j, j-1);        
        }
    }
}

Shell sort

Insertion sort is slow for large unordered arrays because the only exchanges it does involve adjacent entries, so items can move through the array only one place at a time. Shellsort is a simple extension of insertion sort that gains speed by allowing exchanges of array entries that are far apart, to produce partially sorted arrays that can be efficiently sorted, eventually by insertion sort.

The idea is to rearrange the array to give it the property that taking every hth entry (starting anywhere, such as the subarray index [0, h, 2h, 3h…] and [1, h+1, 2h+1,…]) yields a sorted subsequence. By h-sorting for some large values of h, we can move items in the array long distances and thus make it easier to h-sort for smaller values of h. Using such a procedure for any sequence of values of h that ends in 1 will produce a sorted array.

One common decreasing sequence is $(3^k - 1)/2$ starting at the largest increment less than N/3 and decreasing to 1.

C++ implementation:

// shell sort
void shellsort(std::vector<int> &vec)
{
    int n = vec.size();
    int h = 1;
    while (h<n/3)
    {
        h=3*h+1;
    }       
    while (h>=1)
    {
        for (int i = h; i<n; ++i)
        {
            for (int j=i; j>=h && (vec[j]<vec[j-h]); j=j-h)
            {
                exchange(vec, j, j-h);            
            }        
        }    
        h = h/3;
    }
}